Los Angeles Clippers commentator Ralph Lawler has a saying: “First to 100 wins.…
Statistics
More than mean, median, and mode.
-
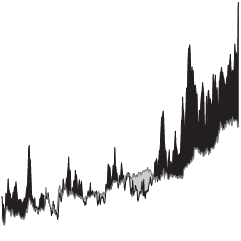
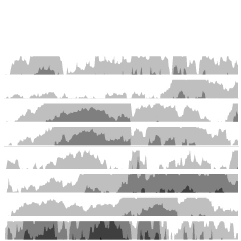
Does the first to 100 points usually win in the NBA?
-
Explore generative models and latent space with a simple spreadsheet interface
Generative models can seem like a magic box where you plug in observed…
-
Exploring data to form better questions
Feeding off the words of John Tukey, Roger Peng proposes a search for…
-
Facial recognition machine for $60
For The New York Times, Sahil Chinoy on privacy and how easy it…
-
FiveThirtyEight evaluates their forecasts
FiveThirtyEight uses forecasts to attach probabilities to politics and sports, and they get…
-
Finding context for the data
Context makes data useful. Without it, it’s easy to get lost in numbers…
-
Census data downloader to reformat for humans
There is a lot of Census data. You can grab most of the…
-
Data for 200M traffic stop records
The Stanford Open Policing Project just released a dataset for police traffic stops…
-
A game to test your ability to pick random numbers
Compared to a computer’s pseudo-random number generator, we are not good at picking…
-
Case of the 500-mile email
Trey Harris, a previous tech administrator for a university, tells the story of…
-
Probability you will break up with your partner
Rosenfeld, et al. from Stanford University ran a survey in 2009 for a…
-
Data-driven porn
Gustavo Turner for Logic on his experiences covering the porn industry and the…
-
Looking for common misspellings
Some words are harder to spell than others, and on the internet, sometimes…
-
When geolocation makes everyone think you stole their phone
People show up unannounced at John and his mother Ann’s home in South…
-
No such thing as raw data
Nick Barrowman on the myth of raw data:
Assumptions inevitably find their way… -
Fake internet
Max Read for New York Magazine describes the fake-ness of internet through the…
-
Following your gut, following the data
The Wall Street Journal highlighted a disagreement between data and business at Netflix.…
-
Spotting AI-generated faces
Computers can generate faces that look real. What a time to be alive.…
-
Apps gather your location and then sell the data
The New York Times takes a closer look at the data that apps…
-
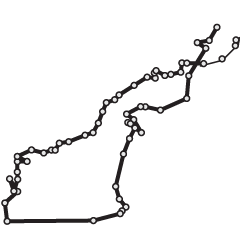
When cycling is faster than driving
Deliveroo is a service that picks up and delivers food. Data from their…











 Visualize This: The FlowingData Guide to Design, Visualization, and Statistics
Visualize This: The FlowingData Guide to Design, Visualization, and Statistics