your.flowingdata got a couple of cool updates recently. One is based on your interactions with others on Twitter and the other helps you find relationships in your actions.
Twitter Mentionmap
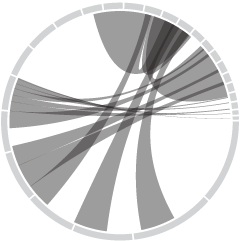
The first is the Twitter Mentionmap created by Daniel McLaren. It’s a network visualization (above) that lets you explore how you (or other Twitter users) interact with others.
It’s not focused on the data that many of you are used to seeing on YFD, but it’s always been my plan to bring in other data sources. So when I saw Daniel post the original Mentionmap, I jumped at the chance to get a version for YFD. It seemed like a good first step to branching out. Get it? Network, branching out. Oh nevermind.
By the way, Daniel used his constellation framework to build this. It’s called asterisq. It’s worth a look if you’re looking to visualize network data. Daniel can also help you with customization and design.
Read More


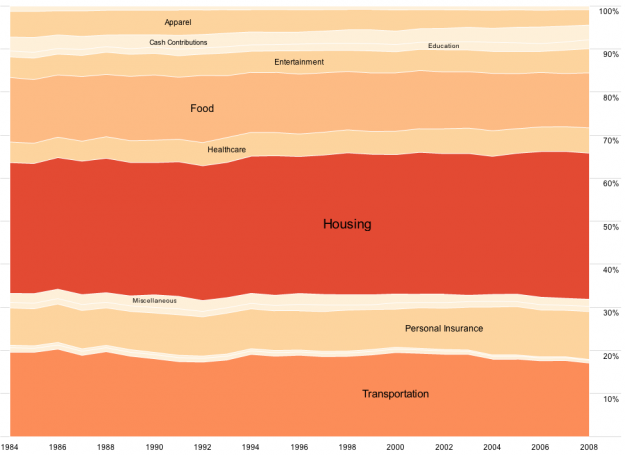
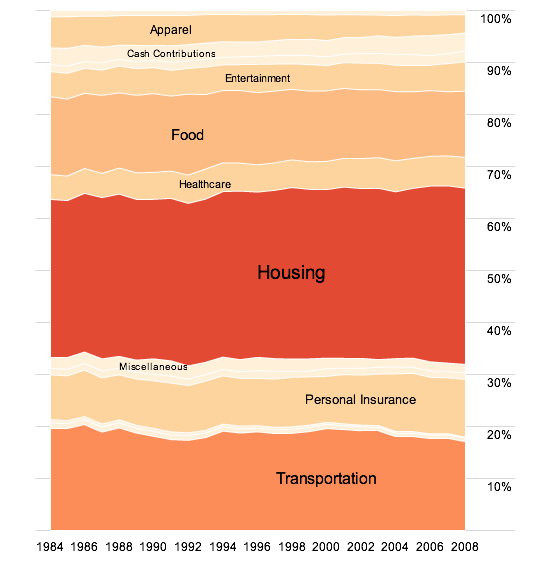
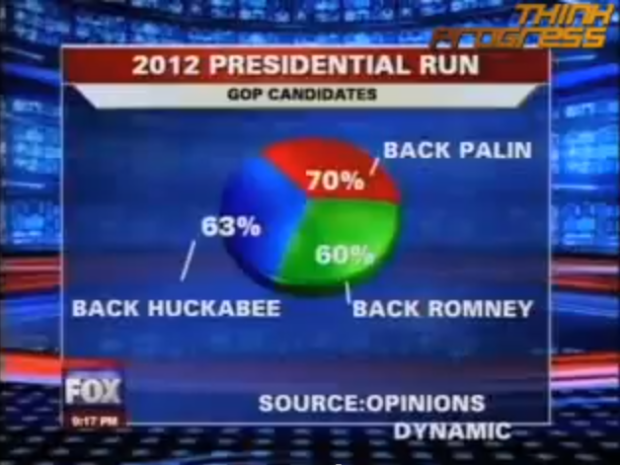
 Visualize This: The FlowingData Guide to Design, Visualization, and Statistics (2nd Edition)
Visualize This: The FlowingData Guide to Design, Visualization, and Statistics (2nd Edition)