Why does it almost always seem like you’re in the slow line at the grocery store or in the driving lane with the most cars on the freeway? Bill “Engineer Guy” Hammack explains in terms of queuing theory in the video below:
Bill reveals how “queueing theory” – developed by engineers to route phone calls – can be used to find the most efficient arrangement of cashiers and check out lines. He reports on the work of Agner Erlang, a Danish engineer who, at the opening of the 20th century, helped the Copenhagen Telephone Company provide the best level of service at the lowest price.
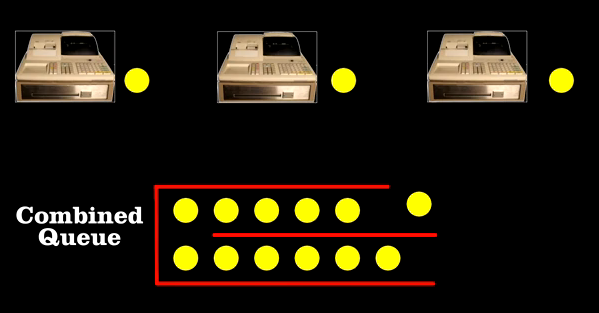
Erlang found out how many telephone lines the company needed, given the average number of calls per hour. Similarly, you can figure out how many checkout lines you need, given the average number of customers. It turns out the best arrangement is to have a single line, and the next customer goes to the next available register. There’s less chance of blockage from a single delay.
But people don’t like doing that apparently, and so assuming random selection, ending up in the slow line comes down to simple probability.
Another way to think about this problem is in terms of time. You wait when you’re in a slow line. You move when you’re in a fast line. So the longer amounts of time spent waiting feel more significant (even though it might be a single pick) than when you made the fast picks.
[Engineer Guy via Revolutions]
When queueing I always choose a line on the side, never in the center. In the center, there are two lines next to me. The probability that one of these lines is faster than mine is 66.7%. On the side that probability drops to 50%.
Umm, there are still 2 lines “next” to you; simply 2 to your left or 2 to your right…the probability another lane is faster is still 66.7%
The example in the video refers to the total # of permutations for all lanes in which your line only takes the lead. It doesn’t matter which lane you pick when 3 lanes are available since there will always only be 2/6 times that lane takes the lead.
In fact, generally speaking, it doesn’t even matter if one of the cashiers is exceptionally fast or slow since Erlang’s model assumes speed at any lane is random. But, certainly does matter while you’re standing in line :D
people in south africa don’t seems to mind as it visibly looks faster because the line keeps moving because of the multiple tellers.
Single queue, multiple servers always provides the lowest average wait time. Banks learned this long ago. Supermarkets, eh, not so much.
You are only considering one dimension of the problem. Different business, different space use patterns. The single line is a much easier proposition in a big empty space than one organized with functional aisles.
Some branches of Marks&Spencer to a single queue, multiple checkout system. Works very well and noticeably more efficient.
Marcello: The probability looks 75% to me. For lines on both side of yours the possibilities are slow-slow,fast-slow,slow-fast,fast-fast. Only slow-slow is a good option,because only then you are faster than both. So 3 out of 4 options are bad, hence 75% probability. :-)
I think the fallacy is that these events aren’t equiprobable. slow-slow happens a third of the time, fast-fast happens one third, slow-fast and fast-slow happen 1/6 each.
There is a weird hybrid approach used at JFK in particular where you queue in one line but then are assigned to one of the many 2 or 3 person queues in front of the immigration officers. This is probably theoretically quite efficient given the fact that you want to minimise the time that customers realise that the booth (cashier) is empty and then walk to the booth. However, in practice it feels frustrating and annoying.
Excellent analysis of the JFK approach. We have an application at work that does just that. One big service queue, but each individual server pulls in a couple off the main queue to keep them in hand. The single queue is over JMS and takes milliseconds to pull from while the per server queue takes microseconds thus the actual server is never idle for any appreciable time.
True that it’s efficient but in terms of human response it doesn’t work well. The distribution of waiting times is very skewed. The mean waiting time is almost certainly less and so, on average, I get through JFK more quickly although I probably don’t notice the 20 seconds shaved off the time (but JFK does because they can employ less immigration staff). What I notice is when I get assigned to a queue behind some bloke without a passport or who is drunk and then I get the extreme skewed waiting time of 20/30 minutes.
Fast efficient exception handling is probably the key here.
Pingback: Marry Christmas | Tynybyte
Pingback: DYSPEPSIA GENERATION » Blog Archive » Why the other lines always seem to move faster than yours
Part of my multiple-line strategy is to predict the probable behaviours of line members. Too many times older people (I am one) feel an obligation to find exact change, an exercise that inevitably adds to transaction processing time. In the same vein, shoppers with children seem prone to longer transaction times. I also try to avoid bored cashiers who are desperate for conversation, since I inevitably end up behind a bored patron with the same need.
iI also know of the totally non-logical approach to delays in the checkout line.Instead of griping about it, always put grapes or some other finger food in your cart.While the store doesn’t give a damn about how much of your valuable time they waste,they save mucho dinero by having less cashiers.AND you might even remember stuff you FORGOT to buy.But if you have a snack ON THEM while in line your time is worth it.Just eat them ALL…..pass some out if you dare.
Marcello: The probability looks 75% to me. For lines on both side of yours the possibilities are slow-slow,fast-slow,slow-fast,fast-fast. Only slow-slow is a good option,because only then you are faster than both. So 3 out of 4 options are bad, hence 75% probability. :-)
Regarding the dislike of the queue methodology I point you to the Letters to the Editor of the Sydney Morning Herald (Australia) on 18 January, 2011:
http://www.smh.com.au/national/letters/time-for-a-tax-to-create-a-longterm-disaster-fund-20110117-19u22.html
Irrespective of the speed advantage when using the queue approach, people, particularly those of the middle class and up, are reticent to stand in a queue.
Evidently this person hasn’t experienced the immigration and customs queues of New York’s JFK Airport as I have.
Pingback: CompSci 1 – World 0 « OuttaCtrl