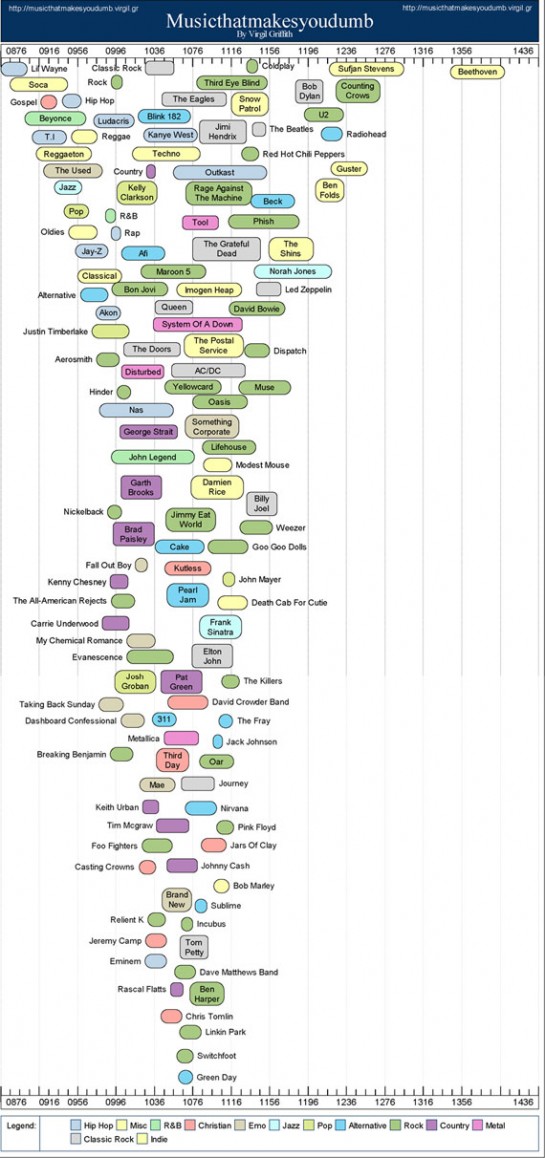
Virgil Griffith, a CalTech graduate student, follows up books that make you dumb with music that makes you dumb. “Dumb” people listen to Lil’ Wayne and “smart” ones listen to Beethoven, that is, if you believe that SAT is a good judge of smarts. I’m not sure if this is actually new or just became popular again because it was in the WSJ. Virgil put up the book version over a year ago. Oh well, it’s Friday. I’m personally all over the board on this one. What kind of music do you like?
[via beatcrave | Thanks, Tim]

 Visualize This: The FlowingData Guide to Design, Visualization, and Statistics (2nd Edition)
Visualize This: The FlowingData Guide to Design, Visualization, and Statistics (2nd Edition)

not a single Electronic music band/DJ/whatever?
*amazing* fact.
ie, you are doomed ;)
WEEZY, BABY
kodisha, I’m perplexed too. Electronica is popular enough by now that it ought to be quantifiable. No Shpongle? Not even an entry for The Orb or Chemical Brothers? If I had been included on that chart I would be in that big blank area behind Beethoven listing, with my thumping sound system. :) Maybe the blank area is where the techno fans would have been?
doubt the causality this data suggests. Dumb people simply like bad music…LOL
Pete Seeger will make you dumb enough to go communist. He even beats Peter, Paul, and Mary for dumbitude.
There is an entry for techno… below Blink and Kanye West.
Too bad they don’t have SAT scores of the musicians themselves. I’m sure Lil’ Wayne would still be at the bottom!
Big Radiohead fan, but I didn’t score what the graph implies. People who like jazz/gospel appear to be kind of screwed here.
this is the stupidest thing ive ever seen
Yes, I know it’s anecdotal and not data, but I don’t know a single dumb person who likes jazz. And I know a lot of dumb people and a lot of people who like jazz. Meh.
This music doesn’t make you dumb (or lead to poor standardized test scores), people who have low SAT scores are more likely to listen to this music. There are also some serious socioeconomic issues raised by this graphic (not to mention some value laden thoughts on the SAT). Leave it to the WSJ to make such backwards and specious correlations
Would be cool to see this the other way around, i.e. people who listen to X are most likely to get score Y.
Do I have to be the one to pull out the old “correlation is not causation” chestnut here?
this chart makes you dumb
Pingback: Brush away the cobwebs from your daydreams » Blog Archive » links for 2009-04-03
Pingback: Music That Makes You Dumb
While clearly this is a prime example of correlation is not causation, I do find it interesting that Christian music scores particulary low
They Might Be Giants and XTC must have fallen off the right hand of the chart.
And where’s Electric Light Orchestra?
Pingback: Attention Music Lovers - especially those with a predilection for Sufjan Stevens and Beethoven! « The Porphyrogennetos
Dumb people listen to “jazz” – this is ridiculous.
Pingback: Infographic: Music that makes you dumb
Come on. Cake? Mediocre? apparantly people listening aren’t paying much attention to McCrea’s message. And ‘beat out’ by Jack all-sounds-the-same Johnson???
Led Zepplin? About the most overplayed band ever. What age group is this? If you track the baby-boom generation, the folks STILL listening are the ones at the I-don’t think-much-about-stuff end of the scale.
Although, the comment about who IS listening to this music makes a point. This popularity contest basically relies on commercial radio stations. And you have to be brain-dead to listen to that for more than 5 minutes in a sitting.
Long live Indie!
So only people who listen to Beethoven score above 1300? This chart says I should have scored at least 350 points lower than I did.
Aside from the obvious problems with his methodology (he’s just correlating average college SAT scores with popularity among students at that college), it’s also a really misleading graphic. The vertical axis means nothing, and the width of the blobs is determined by the standard deviation of that particular musician/genre — which means the more people like that band/genre, the thinner the band you see. So if Country music is most popular at all sorts of colleges, it’ll just show up at a tiny blip in the middle; Beethoven, who is rarely listed, shows up as a big swath (presumably because only Harvard and Princeton students are pretentious enough to list him on Facebook — obviously, real smart people would list Bach instead).
It’s an interesting graphic but really begs a few questions (many already raised by others). I wondered where all the other classical composers, artists are… and then there’s the matter of not only what someone listens to… but how much? I would think a *smart* person would probably have a wider range of musical experience than a *dumber* person…. would be exposed to more and would probably like a variety of musical styles… I don’t think this chart accounts for that variable (one of it’s many failings). I’d be curious if those ranked could only list one musician/style or every one they listen to and if those were ranked from most listened to – to least.
scored a 1440 but apparently should have gotten a 1072 with my love of ben folds, kelly clarkson, pop, oldies, norah jones, maroon 5, jack johnson, green day, switchfoot, third eye blind and carrie underwood
interesting to see which artists have the widest range
This is the stupidest ******* thing I’ve ever seen. So Jazz fans are “dumb”? In what universe? And apparantly you’re “smart” if you listen to pretentious music that appeals to peaky college students in fake glasses and skinny jeans.
Pingback: Garbage in, garbage ou…uh, actually, I guess in this case garbage stays. – Skirl | Dan Dickinson
Pingback: Do You Suffer From Low Intelligence? | learningIT
Pingback: Zach Wise » Daily Digest for 2009-04-11
Oh, dumb people listen to (predominantly) black artists and smart people listen to (predominantly) white artists. Well, I’m sure there’s nothing wrong with that
Pingback: Brush away the cobwebs from your daydreams » Blog Archive » My del.icio.us bookmarks for April 3rd through April 10th
Pingback: Science Etcetera, Venusday 20090417 | ideonexus.com